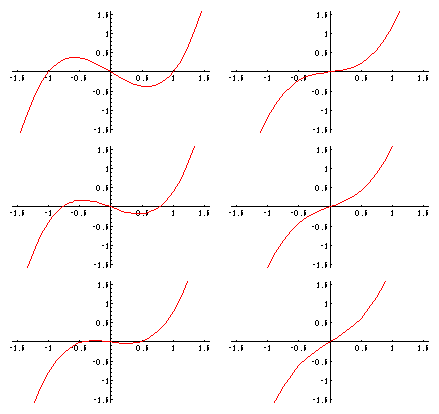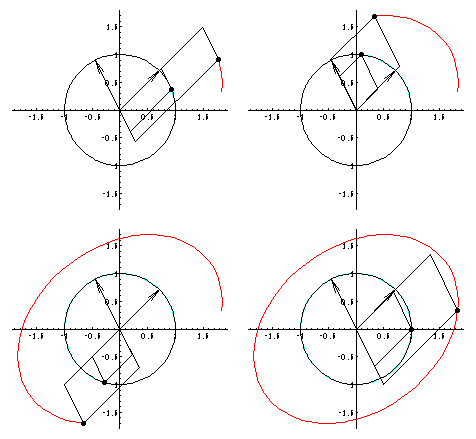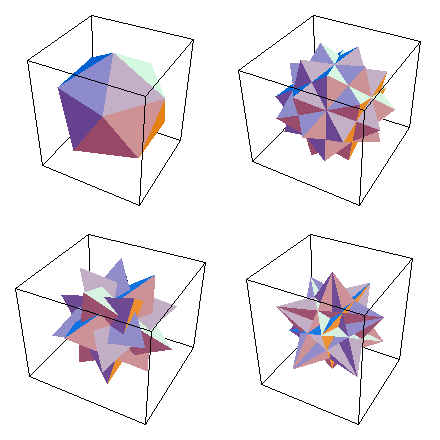Topics of Illustrated Mathematics
Topics of Illustrated Mathematics
Each part of Illustrated Mathematics is listed here with an example. All examples have been produced exclusively with the programs that are part of Illustrated Mathematics.
Since this booklet cannot show true animations, one or several selected graphics are shown.
Additional types of visualizations can be found in the documents that constitute the collection and in the description of the commands.
 Theory of Functions
Theory of Functions
Examples can be found in the Collection notebooks Functions and TrigFunctions.
Notices to the programs are in the Manual notebooks Analysis and TrigFunctions.
 Polynomials and Rational Functions
Polynomials and Rational Functions
The influence of the parameter a in the cubic polynomial x^3 + a x is shown in the sequence of images. The value of a is changed from -1 to 1.
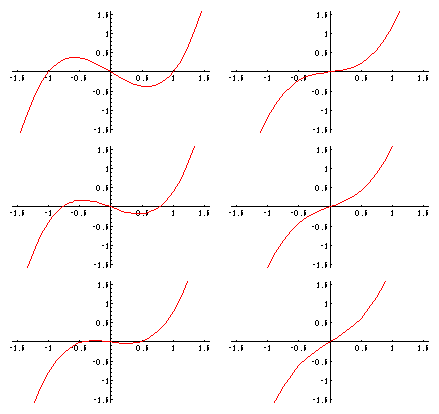
 Trigonometric Functions
Trigonometric Functions
The construction of the sine function with the help of a triangle with hypotenuse 1.
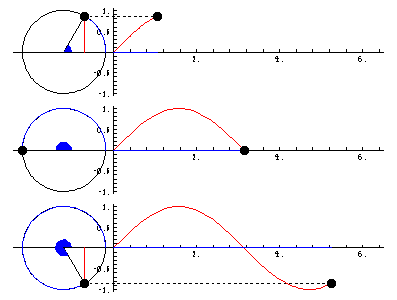
 Exponential and Logarithm
Exponential and Logarithm
Two logarithms, red/dark the natural logarithm and blue/light the logarithm to base 10, as well as two exponentials, e^(-x) (green/light) and 10^(-x) (violet/dark) are shown.
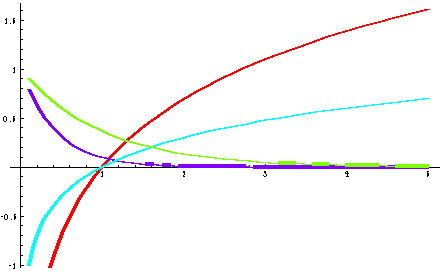
 Sequences and Series
Sequences and Series
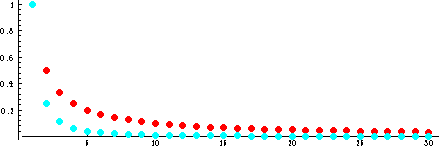
The sequence 1/n (red/dark) converges more slowly toward zero than 1/n^2 (blue/light).
The alternating harmonic series converges toward log 2.
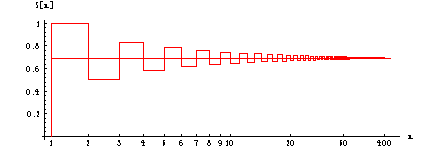
Examples can be found in the Collection notebooks Sequences and Series.
Notices to the programs are in the Manual notebooks Sequences and Series.
 Derivatives
Derivatives
This animation shows how the derivative of a function is constructed. The tangent through the point running along the curve is constructed and translated to the left. There, its slope can be read off and is used to graphically determine the first derivative.
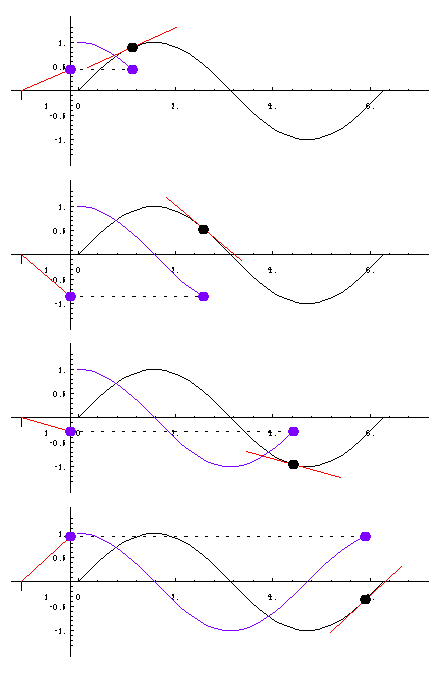
Examples can be found in the Collection notebooks Derivatives and Differential.
Notices to the programs are in the Manual notebook Differentiation.
 Analysis of Functions
Analysis of Functions
The popular topic of discussion of functions can be supported by computer. Here, zeros, extremal values, and points of inflection are computed and shown graphically.
Analysis of the rational function f(x) = x(x-2)(x+2)/(x2+1):
2
x (-4 + x )
Function: -----------
2
1 + x
Symmetry with respect to the origin
Zeros: {-2, 0, 2}
Minima: {( 0.728786,-1.65111 )}
Maxima: {( -0.728786,1.65111 )}
Points of Inflection: {( -1.73205,0.433013 ), ( 0,0 ),
( 1.73205,-0.433013 )}
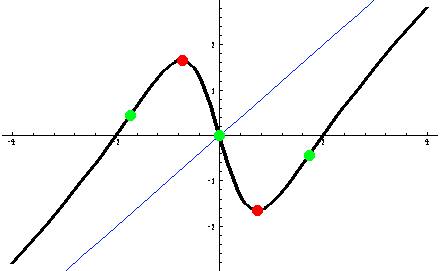
Examples can be found in the Collection notebook Analysis.
Notices to the programs are in the Manual notebook Analysis.
 Integration
Integration
The construction of the integral is demonstrated in this animation. The area under the curve is displayed on the left in the form of a rectangle with base 1. The height of this rectangle is the value of the integral. In the animation, the upper limit of the integral is increased from left to right.
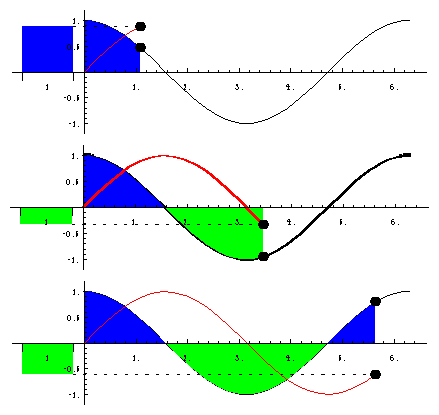
Examples can be found in the Collection notebook Integration.
Notices to the programs are in the Manual notebook Integration.
 Differential Equations
Differential Equations
Examples can be found in the Collection notebooks ODEs, ODEApplications, and ODEAnimations.
Notices to the programs are in the Manual notebook ODEs.
 First-Order Differential Equations
First-Order Differential Equations
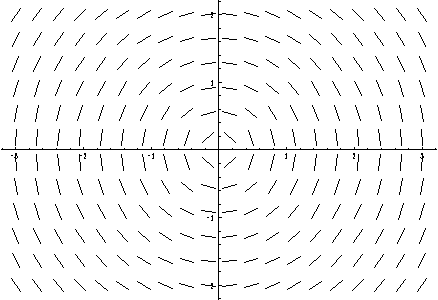
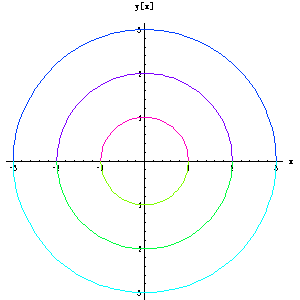
A linear differential equation of first order specifies a direction for each point in a region. It is the tangent direction of the integral curve through this point.
This is the direction field for the equation y' = -x/y.
These are the solutions of y y' + x = 0.
2 2
Solutions: {-Sqrt[-x + C[1]], Sqrt[-x + C[1]]}
 Second-Order Differential Equations
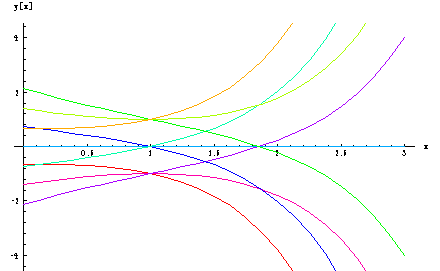
Second-Order Differential Equations
We show the solutions of the differential equation y'' - y' - y = 0 with boundary conditions y(1) = a and y'(1) = b for a,b in {-1,0,1}.
((1 - Sqrt[5]) x)/2 ((1 + Sqrt[5]) x)/2
Solutions: {E C[1] + E C[2]}
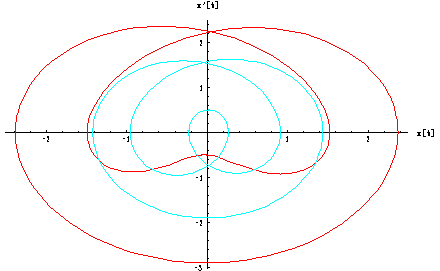
This is a graphic with solutions of cos(3/2 t) = x'' + x in phase space.
3 t
4 Cos[---]
2
Solutions: {C[2] Cos[t] - ---------- - C[1] Sin[t]}
5
 Conic Sections
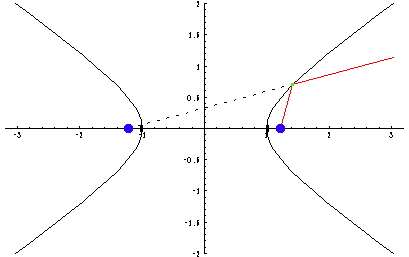
Conic Sections
The zero manifold of a quadratic polynomial in two variables forms a conic section. The characteristics of this (possibly degenerate) conic (its center, apices, focal points, and asymptotes) are computed and shown in the graphic.
Parabolas, ellipses, and hyperbolas as the locus of points that satisfy certain distance constraints can be visualized by an animation.
Reflection properties of these conic sections are also illustrated.
Examples can be found in the Collection notebooks ConicSections, Reflections, and Classification.
Notices to the programs are in the Manual notebook ConicSections.
 Complex Functions
Complex Functions
A complex-valued function requires four real dimensions for visualization (two each for domain and range). This can be achieved in three dimensions by using color as the fourth dimension: the horizontal plane represents the domain (real and imaginary part), the vertical axis shows the absolute value of the function, the color shows the argument according to this key.

This is the identity function f(z) = z.
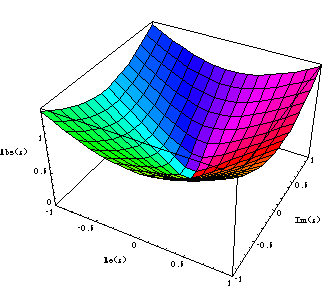
The function f(z) = 1/z^2 has a double pole at z = 0.
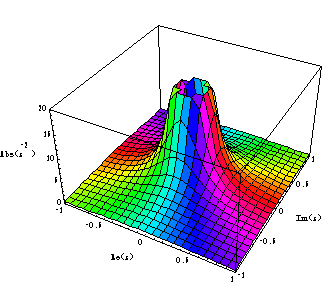
Examples can be found in the Collection notebook ComplexFunctions.
Notices to the programs are in the Manual notebook ComplexFunctions.
 Linear Maps
Linear Maps
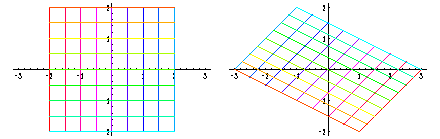
This is the effect of a linear mapping on Cartesian parameter lines.
If a two-dimensional linear map has two real-valued eigenvectors, any point can be written in terms of these and each component can be mapped separately. In an animation, this process can be performed for each point of the unit circle.
M = 1.83333 0.166667
0.333333 1.66667
Eigenvalues: {2., 1.5}
Eigenvectors: {{0.707107, 0.707107}, {-0.447214, 0.894427}}
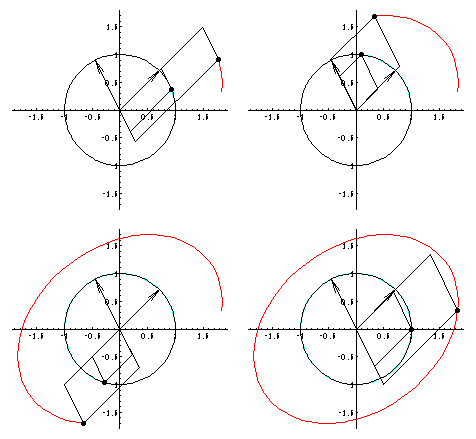
Examples can be found in the Collection notebook LinearMaps.
Notices to the programs are in the Manual notebook LinearMaps.
 Conformal Maps
Conformal Maps
Conformal maps can be visualized using the images of coordinate lines. Here are the polar coordinate lines under the Möbius transform f(z) = (2z-I)/(z-1):
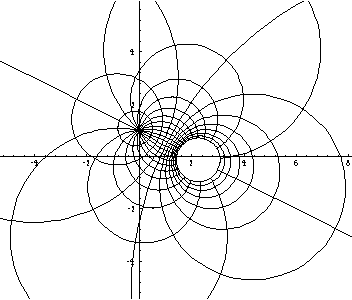
Examples can be found in the Collection notebook Conformal.
Notices to the programs are in the Manual notebook ComplexMap.
 Cycloids and Related Curves
Cycloids and Related Curves
This is a cycloid.

The curve traced by a point with a distance of 0.8 from the center of a circle (radius 1) which rolls in a circle with radius 7/2 is a curtate hypocycloid.
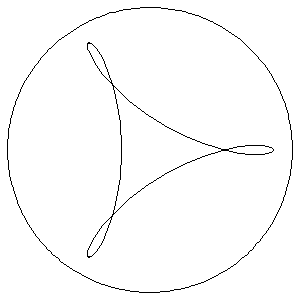
Examples can be found in the Collection notebooks RollingCircles, Cycloids, Hypocycloids, and Epicycloids.
Notices to the programs are in the Manual notebook RollingCircles.
 Figures of Revolution
Figures of Revolution
Cylinder, sphere, torus, Moebius strip, double helix, and so on, are surfaces of revolution. The last two of them are twisted.
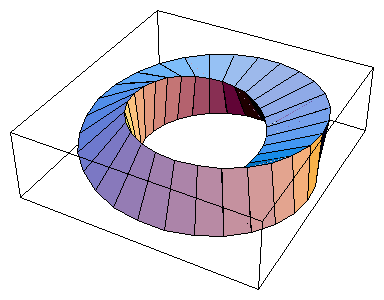
The creation process of such surfaces can be shown by an animation.
Examples can be found in the Collection notebook Revolution.
Notices to the programs are in the Manual notebook Revolution.
 Polyhedra
Polyhedra
There are exactly 75 uniform polyhedra, as well as two infinite families of prisms and antiprisms. This picture shows the 20 convex uniform polyhedra, that is, the five Platonic solids, the thirteen Archimedian polyhedra, as well as one prism and one antiprism.
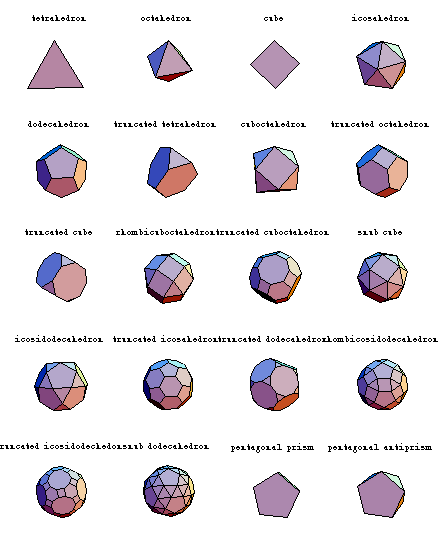
Examples can be found in the Collection notebooks Polyhedra and PolyPictures.
Notices to the programs are in the Manual notebook Polyhedra.
 Icosahedra
Icosahedra
There are 59 stellations of the icosahedron. Here are the original icosahedron, the compound of five octahedra, the commpound of five tetrahedra, and the great icosahedron.
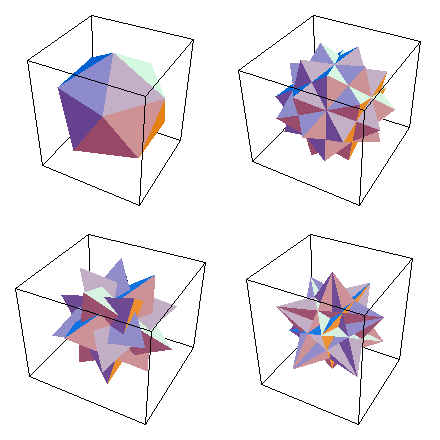
Examples can be found in the Collection notebook Icosahedra.
Notices to the programs are in the Manual notebook Icosahedra.
 Minimal Surfaces
Minimal Surfaces
Minimal surfaces are important in physics and engineering. This picture shows Enneper's surface with polar parameter lines.
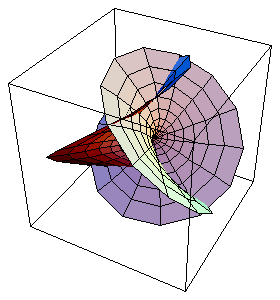
Examples can be found in the Collection notebook MinimalSurfaces.
Notices to the programs are in the Manual notebook MinimalSurfaces.
 Iterated Functions
Iterated Functions
The function f(x) = 4x(1-x) is one of the simplest examples of chaotic behavior. If the function is iterated repeatedly, close initial values are distributed arbitrarily in the interval [0,1].
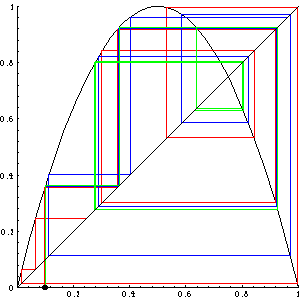
Examples can be found in the Collection notebook Chaos.
Notices to the programs are in the Manual notebook Chaos.
Up to Illustrated Mathematics