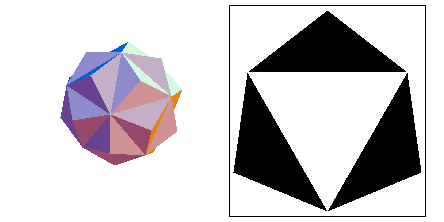
The first stellation is formed by facet 2. It is similar to the figure used at one point by Wolfram Research as its logo (and still used as a Mathematica icon). That figure was wrongly called the ``stellated icosahedron.'' (It should properly be called a faceted icosahedron.)

Here is the great icosahedron, no. 11 in our list. In contrast to the version from Graphics`Polyhedra` this construction generates only the visible parts of the faces and is, therefore, easier to render since no intersections of polygons have to be computed.
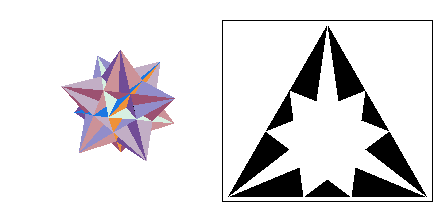
This is the largest of the stellations. It contains facet 13 (which includes 14, as explained
earlier).

No. 8 is the only stellation whose solid pieces are completely disconnected (they do not even share vertices).
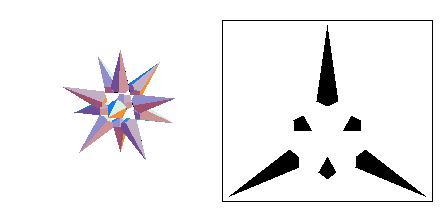
This stellation is the protoypical chiral stellation. Every chiral stellation is obtained by adding these facets (or their reflections) to a reflexible stellation. Note that it is only vertex connected.

This (reflexible) stellation is the only one that consists entirely of chiral parts. It is the combination of no. 33 (shown above) and its mirror image.
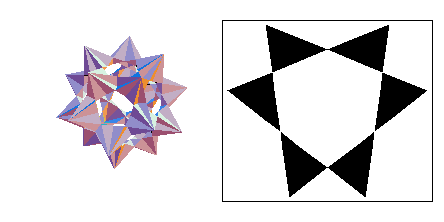
Below are the left and right forms of the compound of five tetrahedra.
Show[ GraphicsArray[{Icosahedra[36], Icosahedra[36, True]}] ];
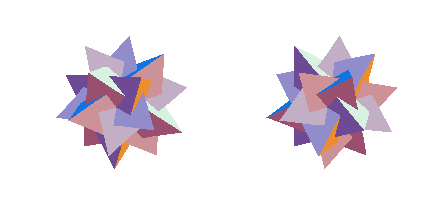
Their combination is another stellation: the compound of ten tentrahedra.
Show[ Icosahedra[18] ];
